Organizing Committee
- Ricardo Cortez
Tulane University - Mark Levi
Pennsylvania State University - Michael Minion
Stanford University - Richard Montgomery
University of California - Santa Cruz
Abstract
Interested in discussing cutting edge research ideas with both peers and leaders in their field?
Interested in broadening your professional network across the mathematical sciences?
Interested in the opportunity to present your ideas and hear about funding opportunities from program officers?
Idea-Lab invites 20 early career researchers (postdoctoral candidates and assistant professors) to ICERM for a week during the summer. The program will start with brief participant presentations on their research interests in order to build a common understanding of the breadth and depth of expertise. Throughout the week, organizers or visiting researchers will give comprehensive overviews of their research topics. Organizers will create smaller teams of participants who will discuss, in depth, these research questions, obstacles, and possible solutions. At the end of the week, the teams will prepare presentations on the problems at hand and ideas for solutions. These will be shared with a broad audience including invited program officers from funding agencies.
IdeaLab applicants should be at an early stage of their post-PhD career. A CV, research statement, and two reference letters are required.

"The best part of the program was meeting and getting to know the other participants - everyone involved was enthusiastic and friendly, and having such a wide range of expertise made it a safe space in which to admit to not knowing particular things and to ask questions and learn from one another. The topic gave us a common ground from which to spark scientific discussions which were both educational and fun."
-- IdeaLab Participant
Confirmed Speakers & Participants
Talks will be presented virtually or in-person as indicated in the schedule below.
- Speaker
- Poster Presenter
- Attendee
- Virtual Attendee
-
Roza Aceska
Ball State University
-
Alessandro Arsie
University of Toledo
-
Brian Benson
University of Illinois at Urbana-Champaign
-
Yougan Cheng
University of Minnesota
-
Ricardo Cortez
Tulane University
-
William Cousins
Massachusetts Institute of Technology
-
Jim Curry
National Science Foundation
-
Marcelo Disconzi
Vanderbilt University
-
Amit Einav
University of Cambridge
-
Fariba Fahroo
DARPA
-
Cristi Guevara
Mexican Petroleum Institute
-
Eric Hall
University of Massachusetts Amherst
-
Silvia Jiménez Bolaños
Colgate University
-
Madison Krieger
Brown University
-
Mark Levi
Pennsylvania State University
-
Lina Ma
Purdue University
-
Reza Malek-Madani
Office of Naval Research
-
Michael Minion
Stanford University
-
Alexey Miroshnikov
University of Massachusetts
-
Richard Montgomery
University of California - Santa Cruz
-
Tomoki Ohsawa
University of Michigan
-
Sarah Olson
Worcester Polytechnic Institute
-
Emily Russell
Harvard University
-
Thomas Russell
National Science Foundation
-
Jason Teutsch
University of Chicago
-
Léon Tine
Institut Camille Jordan, Universite Lyon 1
-
Guowei Yu
University of Toronto
-
Longhua Zhao
Case Western Reserve University
IdeaLab Topics
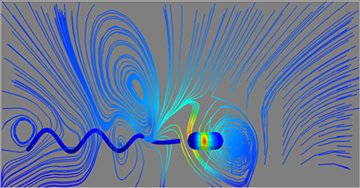
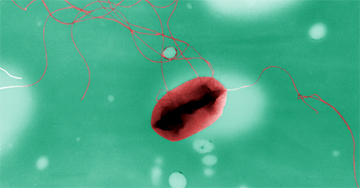
Toward a more realistic model of ciliated and flagellated organisms
The biological world at the scale of cellular organisms is full of fascinating examples of fluid motion that is generated or affected by its interaction with elastic structures. Examples are the fluid motion around "swimming" bacteria and sperm, and the ciliary function in the respiratory system. A common feature of these phenomena is the interaction of elastic flexible membranes or filaments with a surrounding fluid, where the forces generated by the elastic structures and their motion are coupled by the fluid dynamics.
The development of computational methods for the accurate simulation of thin filaments in a fluid has reached maturity. At the same time, the force-generating mechanism of eukaryotic flagella and cilia has been well-studied biologically. However, the vast majority of numerical models of flagellar and ciliary motions do not yet include a proper representation of the internal microtubule structure of flagella.
By bringing together mathematicians with a variety of backgrounds, the goal of this IdeaLab is to brainstorm on possible approaches to introduce a more faithful representation of the internal structure of flagella into a computational model that can be used to study a variety of flows generated by microorganisms.
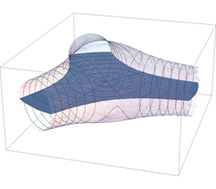
High frequency vibrations and Riemannian geometry
We will discuss several specific projects at the interface of mechanics, geometry and analysis.
The fascinating phenomenon of stabilization by vibration suggests one group of problems. The most famous example of such a stabilization is the Kapitsa pendulum in which the upside-down unstable equilibrium of the standard pendulum becomes a stable equilibrium when the pendulum's pivot is vibrated vertically at a high enough frequency. See, for instance, the YouTube video below.
This effect led to the invention of the cyclotron and of the Paul trap, for which W. Paul received the 1989 Nobel Prize in physics. Another effect in the same spirit is the stabilization of a viscous fluid by vibration. A surface of molasses in an appropriately vibrating container can be made to form a vertical wall! One proposed activity will be to recast these problems in terms of differential geometry, as the study of geodesics on vibrating manifolds. This recasting has not been widely explored despite its important applications.
In celestial mechanics vibrational stablization questions also arise. For example, the equal mass planar three-body problem (a three degree of freedom system after reductions) contains four invariant submanifolds of codimension 2: the collinear three-body problem and its three isosceles sub-problems. These four sub-problems are much better understood than the full planar problem. Oscillations orthogonal to their submanifolds have the potential of connecting the submanifolds in interesting and not well-understood ways. Or perhaps such connections are blocked in some way. From the perspective of differential geometry, we have a Riemannian three-manifold which contains 4 distinguished totally geodesic surfaces. What can we say about the growth or oscillation of the normal mode (orthogonal to the surface) of the Jacobi equation for geodesics lying in one of these surfaces? How does this understanding of normal modes lead to a better understanding of the full geodesic flow?
The discussion will greatly benefit from collaboration of people with diverse interests ranging from geometry to differential equations to mechanics.
Workshop Schedule
Monday, August 11, 2014
| Time | Event | Location | Materials |
|---|---|---|---|
| 9:05 - 9:10am EDT | What is IdeaLab and how to make it work for you - Jeff Hoffstein, Brown University | 11th Floor Lecture Hall | |
| 9:10 - 9:40am EDT | Meet with Introductory Groups | 11th Floor Lecture Hall | |
| 9:40 - 10:40am EDT | Introductory Group Presentations | 11th Floor Lecture Hall | |
| 10:40 - 11:00am EDT | Coffee/Tea Break | 11th Floor Collaborative Space | |
| 11:00 - 12:00pm EDT | Overview (Toward a more realistic model of ciliated and flagellated organisms) | 11th Floor Lecture Hall | |
| 11:00 - 12:00pm EDT | Overview (High frequency vibrations and Riemannian geometry) | 10th Floor Classroon | |
| 12:00 - 1:15pm EDT | Lunch@ICERM | 11th Floor Collaborative Space | |
| 1:15 - 2:45pm EDT | Specialized Talk I (High frequency vibrations and Riemannian geometry) | 11th Floor Lecture Hall | |
| 1:15 - 2:45pm EDT | Specialized Talk I(Toward a more realistic model of ciliated and flagellated organisms) | 10th Floor Classroon | |
| 2:45 - 3:15pm EDT | Coffee/Tea Break | 11th Floor Collaborative Space | |
| 3:15 - 4:15pm EDT | Specialized Talk II (High frequency vibrations and Riemannian geometry) | 10th Floor Classroom | |
| 3:15 - 4:15pm EDT | Specialized Talk II(Toward a more realistic model of ciliated and flagellated organisms) | 11th Floor Lecture Hall | |
| 4:15 - 5:00pm EDT | Questions, Discussion and Brainstorming (High frequency vibrations and Riemannian geometry) | 10th Floor Classroom | |
| 4:15 - 5:00pm EDT | Questions, Discussion and Brainstorming (Toward a more realistic model of ciliated and flagellated organisms) | 11th Floor Lecture Hall | |
| 5:00 - 6:30pm EDT | Welcome Reception | 11th Floor Collaborative Space |
Tuesday, August 12, 2014
| Time | Event | Location | Materials |
|---|---|---|---|
| 8:30 - 9:00am EDT | Touch base and light breakfast | 11th Floor Collaborative Space | |
| 9:00 - 11:00am EDT | Additional Brainstorming Session re: Projects and Group Formation (High frequency vibrations and Riemannian geometry) | 11th Floor Conference Room | |
| 9:00 - 11:00am EDT | Additional Brainstorming Session re: Projects and Group Formation (Toward a more realistic model of ciliated and flagellated organisms) - Meet with faculty leaders and form groups | 10th Floor Classroom | |
| 11:00 - 12:00pm EDT | Work in Groups | ||
| 12:00 - 1:30pm EDT | Break for Lunch & Free Time | ||
| 1:30 - 4:30pm EDT | Working Groups | ||
| 4:30 - 5:00pm EDT | Reconvene to touch base (Toward a more realistic model of ciliated and flagellated organisms) | 10th Floor Classroom | |
| 4:30 - 5:00pm EDT | Reconvene to touch base (High frequency vibrations and Riemannian geometry) | 11th Floor Conference Room |
Wednesday, August 13, 2014
| Time | Event | Location | Materials |
|---|---|---|---|
| 8:30 - 9:00am EDT | Touch base and light breakfast | 11th Floor Collaborative Space | |
| 9:00 - 12:00pm EDT | Working Groups | ||
| 12:00 - 1:30pm EDT | Break for Lunch & Free Time | ||
| 1:30 - 4:30pm EDT | Working Groups | ||
| 4:30 - 5:00pm EDT | Reconvene to touch base (High frequency vibrations and Riemannian geometry) | 10th Floor Classroom | |
| 4:30 - 5:00pm EDT | Reconvene to touch base (Toward a more realistic model of ciliated and flagellated organisms) | 11th Floor Conference Room |
Thursday, August 14, 2014
| Time | Event | Location | Materials |
|---|---|---|---|
| 8:30 - 9:00am EDT | Touch base and light breakfast | 11th Floor Collaborative Space | |
| 9:00 - 12:00pm EDT | Working Groups | ||
| 12:00 - 1:30pm EDT | Break for Lunch & Free Time | ||
| 1:30 - 4:30pm EDT | Working Groups | ||
| 4:30 - 5:00pm EDT | Reconvene to touch base (Toward a more realistic model of ciliated and flagellated organisms) | 10th Floor Classroom | |
| 4:30 - 5:00pm EDT | Reconvene to touch base (High frequency vibrations and Riemannian geometry) | 11th Floor Conference Room |
Friday, August 15, 2014
| Time | Event | Location | Materials |
|---|---|---|---|
| 10:00 - 10:10am EDT | Opening Remarks - Homer Walker, Deputy Director, ICERM | 11th Floor Lecture Hall | |
| 10:10 - 11:25am EDT | Group Presentation 1 | 11th Floor Lecture Hall | |
| 11:25 - 11:45am EDT | Coffee/Tea Break | 11th Floor Collaborative Space | |
| 11:45 - 1:00pm EDT | Group Presentation 2 | 11th Floor Lecture Hall | |
| 1:00 - 2:15pm EDT | Lunch and Informal Discussions (lunch provided at ICERM) | 11th Floor Lecture Hall | |
| 2:15 - 3:30pm EDT | Program Officer Panel | 11th Floor Lecture Hall | |
| 3:30 - 3:40pm EDT | Group Photo in Lecture Hall | 11th Floor Lecture Hall | |
| 3:40 - 4:40pm EDT | Afternoon for Discussions | 11th Floor Collaborative Space |
