Aimed at a general audience, ICERM's "MathBytes@ICERM" series introduces math topics in unique 10-20 minute clips. The videos feature ICERM public lecturers or program visitors who are able to communicate their research interests in concise and often fun ways. Click on the videos below to view our collection.
"Change Ringing: The Beautiful Intersection Between Math and Music"
MathByte featuring featuring Emily Russell, ICERM Postdoctoral Fellow [18 mins]The Beautiful Intersection Between Math and Music in the form of English bell ringing, a tradition from the early 1600's. The bell ringing tradition is very deeply rooted in the mathematics of group theory. In fact, there have been mathematical theorems proven which are very much drawn out of bell ringing.
Emily Russell completed her PhD in Physics at Harvard University under the supervision of Professor David Weitz. Her research interests lie in describing how local interactions drive the global structure and behavior of complex systems; during her PhD work, she examined such phenomena experimentally in charged colloidal systems, and she now focuses on combining her physical intuition with a mathematical understanding of more general systems.
"The Fibonacci Sequence and Fractals"
MathByte featuring Sarah Koch of University of Michigan [20 mins]The Fibonacci sequence is ubiquitous not only in mathematics, but also in nature. From the spiral patterns in pinecones to the Mona Lisa, Fibonacci numbers are everywhere. In this MathByte, we discover the Fibonacci sequence hiding inside the Mandelbrot Set, another famous mathematical object.
Sarah C. Koch is an Assistant Professor in the Mathematics Department at the University of Michigan, and a 2013 Sloan Research Fellowship recipient. (April 2015)
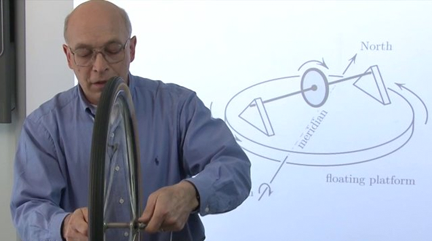
"Paradoxical Mechanical Phenomena"
MathByte featuring Mark Levi of Penn State [12 mins]Mark Levi's area of research is differential equations, dynamical systems and geometry, often related to physical phenomena. One of his hobbies is creating and collecting physical devices that he uses to illustrate mathematical phenomena. Another hobby is inventing and collecting physical solutions to mathematical problems. As a result, he authored two books: "The Mathematical Mechanic: Using Physical Reasoning to Solve Problems" and "Why Cats Land on Their Feet: And 76 Other Physical Paradoxes and Puzzles". In this video, Levi demonstrates two paradoxical mechanical phenomena, both explained, in an unexpected way, by centrifugal force. (March 2014)
"Coloring Critical Points"
MathByte featuring Brown University's Thomas Banchoff [17 mins]Coloring critical points is one of the exercises in visualization that takes place in almost every mathematics course, both in secondary school and in college. Ultimately we want to use calculus to study critical points, but the beginning questions about critical points takes place in algebra during the first and secondary school years. In this “MathBytes” video, Professor Tom Banchoff discusses several visualization examples to show how to generalize them for future use in calculus using not only just one variable, but also two variables. (January, 2014)
"Coloring Critical Points"
MathByte featuring ICERM's "Toy Models" public lecturer Tadashi Tokieda of Cambridge University [24 mins]One of Tadashi Tokieda's lines of activity is inventing, collecting, and studying toys - objects from daily life that can be found or made in minutes, yet which, if played with imaginatively, reveal behaviors so surprising that they intrigue scientists for weeks. In this video you see Tokieda demonstrating a magic routine which is easy to perform yourself and which is a pleasant example of such "toys". (November, 2013)
"Scratching the Surface in Dynamic Visual Effects"
MathByte featuring ICERM public lecturer Robert Bridson of UBC Computer Science [11 mins]Computational physics now underlies some of the most amazing and routine visual effects work. It utilizes numerical models to simulate reality and more on the computer. Natural-looking water, smoke, fire, and clothing effects in film are often handled best by understanding and solving the physics of how they move in nature. Efficient and artist-friendly simulations remain a huge challenge. In this "MathBytes" 10 minute video, Dr. Bridson discusses the general context of physics-based animation in graphics. He also focuses particularly on the advent of new geometric and numerical algorithms for exploiting surface meshes in simulation - both the obvious like clothing and the more surprising like smoke. (March 2013)